Default Survey

Default survey - Oil producers Default survey - Water injectors
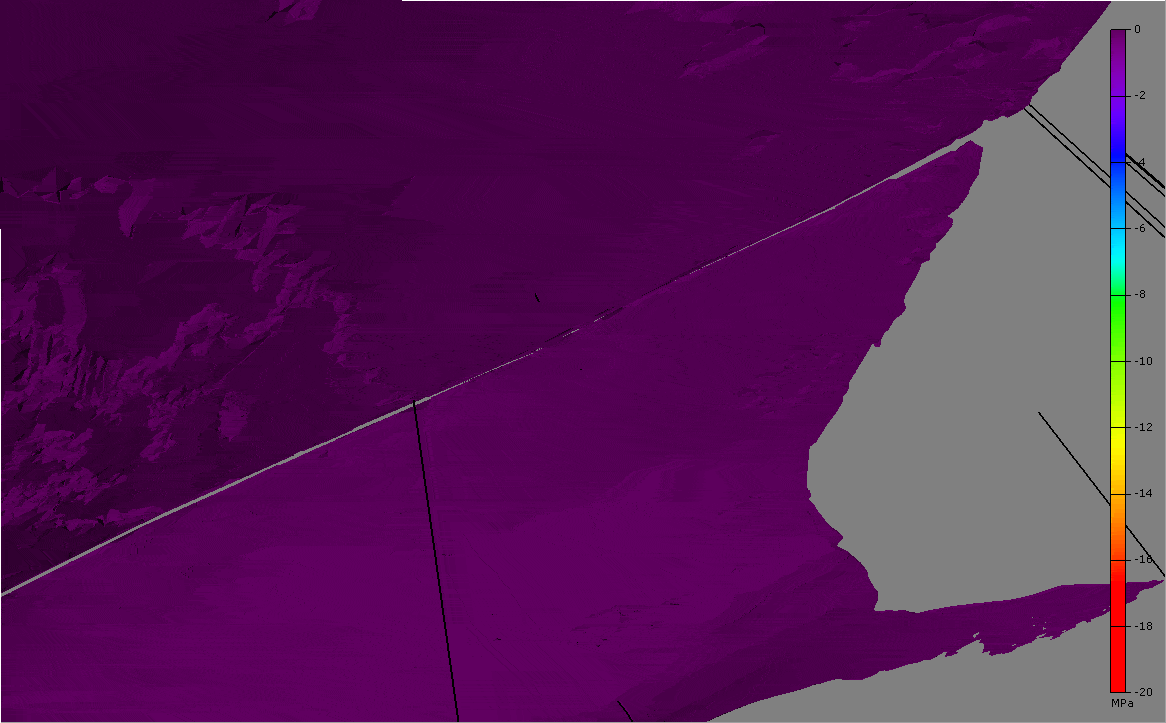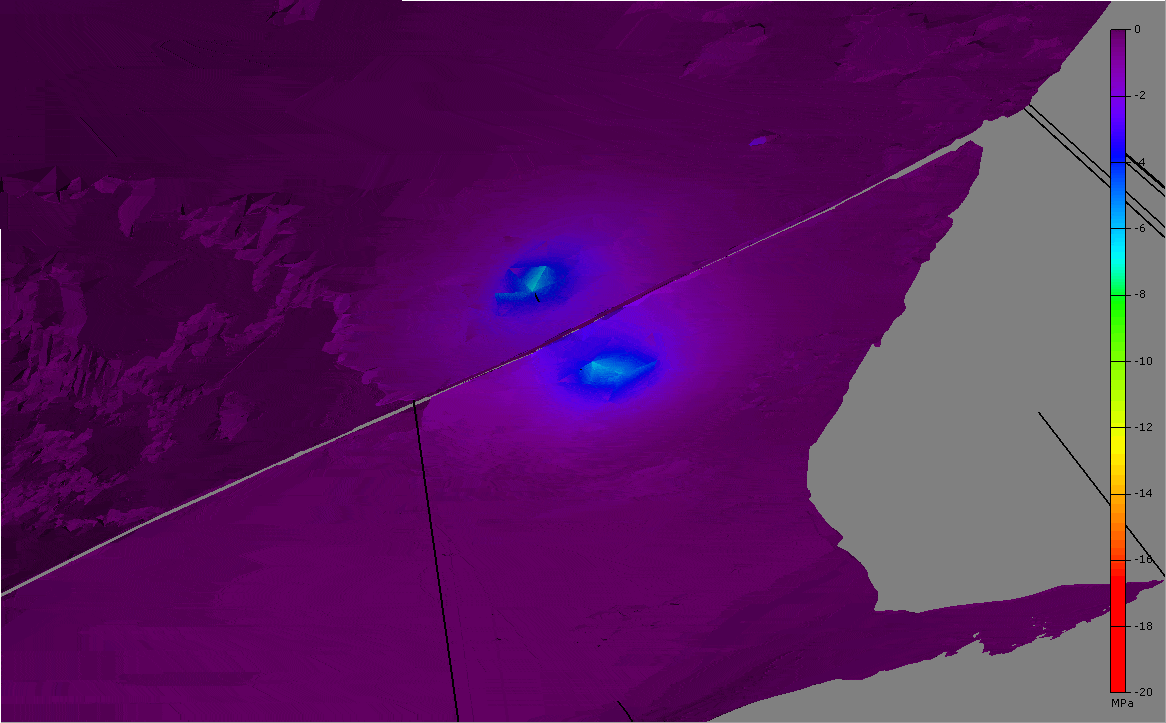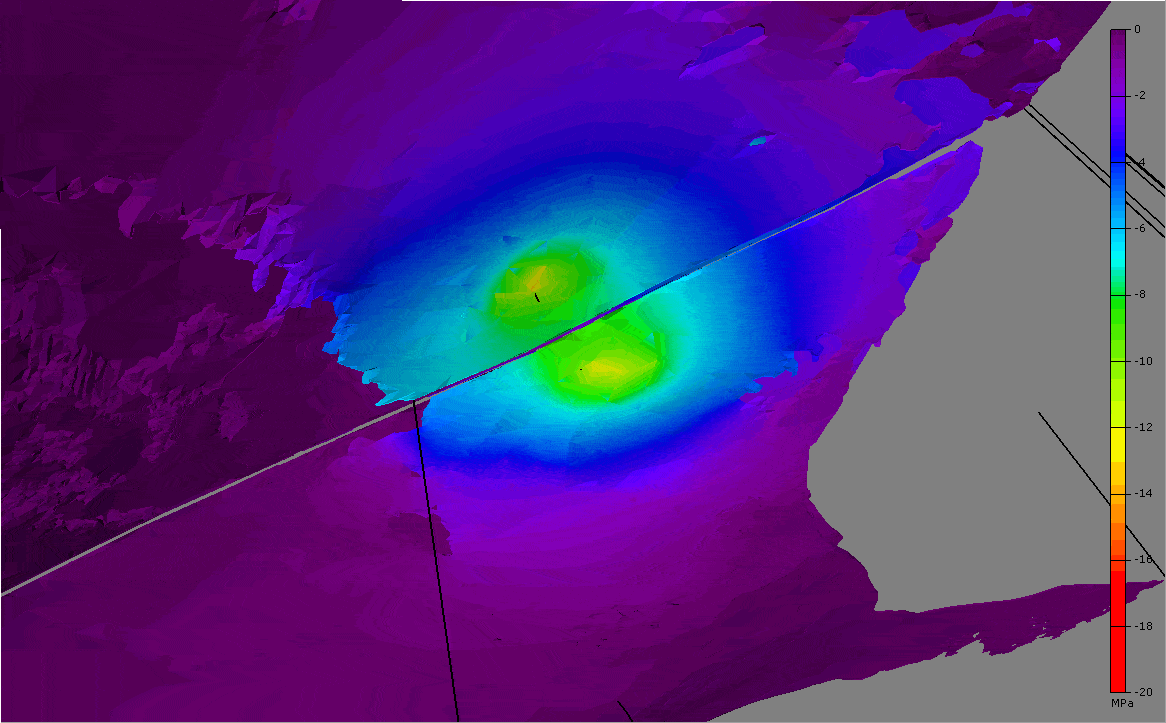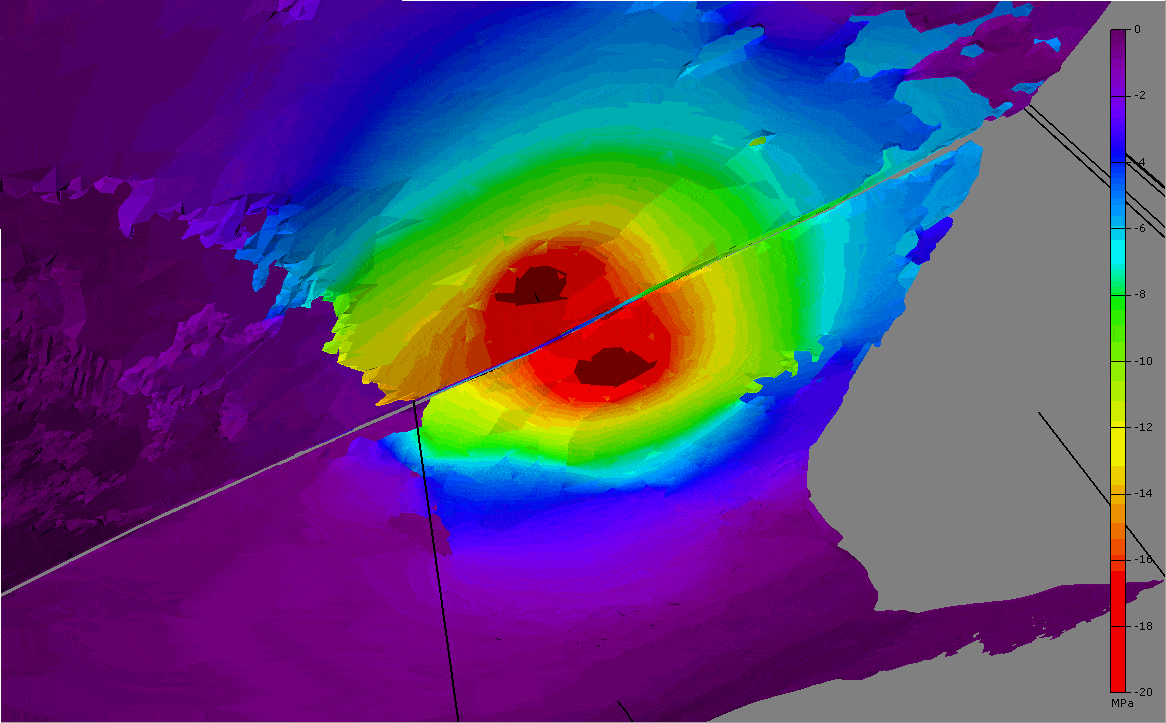
The initial overpressure in the SCA reservoir allows realistic near well draw-downs on the order of 20-25MPa near the wells. In order to have flexibility with the pressure drop in the SCA reservoirs during this and subsequent phases of the field exploitation we assumed pressure lift devices for each of the three well bundles. The pressure depletion during this phase did not require lift devices. While pressure support for the SCA reservoirs is invisioned in the second phase it will require certain amount of time to balance the production wells. Therefore, lift devices may become necessary during the next phases of production. For that reason all relevant well controls flow/pressure gauges are located at the sea floor. All subsequent references to well pressure are with respect to these gauges.

days 0 1095 1460 2555 3650
The well bundles are operated under the following flow control:
SCA_A x3 4000 3000 3000 3000 3000
SCA_B x3 (*) 8000 5000 5000 5000 5000
SCA_C x3 16000 10000 10000 10000 10000
SFR1_E 7000 3500 → 7000 7000
SFR1_W 6000 3000 → 6000 6000
SFR2_E 4000 2200 → 4400 4400
SFR2_W 6000 3100 → 6200 6200
SFR3_E 1000 600 → 1000 1000
SFR3_W 4000 3000 → 5000 5000
The water injectors are operated under the following flow control:
SCA_WI1 30000 30000 30000
SCA_WI2 30000 25000 → 27500 25000
SCA_WI3 40000 40000
SCA_WI4 5000 5000 5000

(*) SCA_B_2 becomes gas injector after phase 2.

Oil Density

Default-Oil-Density
Reservoir
 Depth [m] Pressure [MPa] Bubble Point Pressure [MPa] ρ [kg/m3]
SFR-1E 3720 44.35 34.35 855
SFR-1W 4540 54.12 44.12 835
SFR-2E 3680 43.87 33.87 856
SFR-2W 4260 50.78 40.78 842
SFR-3E 3580 42.68 32.68 859
SFR-3W 4150 49.47 39.47 844
SCA 8140 105.69 50.08 614

SCA Pressure near wells

SCA A Hub

Pressure Change
First Survey SCA-A-Hub-Default
Top View
SCA-A-Hub-Default
Bottom view
SCA-A-Hub-Default

SCA B Hub

Pressure Change
First Survey SCA-B-Hub-Default
Top View
SCA-B-Hub-Default
Bottom view
SCA-B-Hub-Default

SCA C Hub

Pressure Change
SCA-C-Hub-Default
Top View
SCA-C-Hub-Default
Bottom view
SCA-C-Hub-Default

SFR Pressure near wells

Top View
SFR-Hub-Default
Bottom view
SFR-Hub-Default

Monitor 1

During the this phase only the 9 SCA wells are operated for a period of three years from 01-01-2020 until 31-12-2022.

  • SCA-A: 4000 bpd decreasing linearly to 3000 bpd.
  • SCA-B: 8000 bpd decreasing linearly to 5000 bpd.
  • SCA-C: 16000 bpd decreasing linearly to 10000 bpd.

    • The results below are reported at the final time of the simulation (31-12-2022). Wherever available 3D VRML plots are also provided.

    Downloads

    Pressure

    The pressure is computed using modified Arnold-Brezzi finite elements. This a nonconforming Courzeix-Raviart element modified with an additional quadratic bubble which ensures local conservation of mass in each tetrahedron. The local space contains the full linear polynomial space and as consequence it provides second order accuracy. In contrast finite volume methods use piecewise constant pressure in each cell and are only first order accurate.

    Pressure @1195 days
    First Survey Pressure

    View as VRML97

    (plugin such as Cortona3D is required).

    Pressure Change @1195 days
    First Survey Pressure Change

    View as VRML97

    (plugin such as Cortona3D is required).

    Displacement

    The displacements are approximated using standard conforming linear finite elements. They are continous across element boundaries and second order accurate.

    Displacement X @1195 days
    First Survey Displacement X
    Displacement Y @1195 days
    First Survey Displacement Y
    Displacement Z @1195 days
    First Survey Displacement Z

    Strains

    The strains are derived directly from the displacements and are piecewise constant in each element.

    Strain[1,1] @1195 days
    First Survey Strain [1,1]
    Strain[1,2] @1195 days
    First Survey Strain [1,2]
    Strain[1,3] @1195 days
    First Survey Strain [1,3]
    Strain[2,2] @1195 days
    First Survey Strain [2,2]
    Strain[2,3] @1195 days
    First Survey Strain [2,3]
    Strain[3,3] @1195 days
    First Survey Strain [3,3]

    Principal Stress

    The principal stresses are derived directly from the FEM approximation of the displacements and the material properties. They are piecewise linear in each element which is the way the Young modulus and Poisson ratio are interpolated on the computational grid. However, due to the underlying discontinuity of the strains, they are discontinuous across element boundaries. >

    Minimal Principal Stress @1195 days
    First Survey Minimal Principal Stress
    Intermediate Principal Stress @1195 days
    First Survey Intermediate Principal Stress
    Maximal Principal Stress @1195 days
    First Survey Maximal Principal Stress

    Total Stress

    The total stress tensor components are postprocessed in order to gain one order of accuracy. This is done by first constructing the piecewise constant stresses in each element. The stress components are then interpolated in each vertex utilizing stereoscopic angle weights. This results in a piecewise linear, continuous stress field. These postprocessed stress components can be utilized to compute more accurate principal stresses which are continuous across element boundaries.

    Total Stress[1,1] @1195 days
    Total Stress[1,1]
    Total Stress[1,2] @1195 days
    Total Stress[1,2]
    Total Stress[1,3] @1195 days
    Total Stress[1,3]
    Total Stress[2,2] @1195 days
    Total Stress[2,2]
    Total Stress[2,3] @1195 days
    Total Stress[2,3]
    Total Stress[3,3] @1195 days
    Total Stress[3,3]

    Saturations

    The saturations are resolved using an explicit first order FV method. They are piecewise constant in each cell. A MAPR linear reconstruction may be uploaded at a later stage.

    Water Saturation @1195 days
    Water Saturation

    View as VRML97

    (plugin such as Cortona3D is required).

    Oil Saturation @1195 days
    Oil Saturation

    View as VRML97

    (plugin such as Cortona3D is required).

    Water Saturation Change @1195 days
    Water Saturation Change

    During this phase only the 9 SCA wells are operated for a period of four years from 01-01-2020 until 31-12-2023.

  • SCA-A: 0 - 3 years : 4000 bpd decreasing linearly to 3000 bpd. 4 year : Constant rate - 3000 bpd.
  • SCA-B: 0 - 3 years : 8000 bpd decreasing linearly to 5000 bpd. 4 year : Constant rate - 5000 bpd.
  • SCA-C: 0 - 3 years : 16000 bpd decreasing linearly to 10000 bpd. 4 year : Constant rate - 10000 bpd.

    • The results below are reported at the final time of the simulation (31-12-2023). Wherever available 3D VRML plots are also provided.

    Downloads

    Pressure

    The pressure is computed using modified Arnold-Brezzi finite elements. This a nonconforming Courzeix-Raviart element modified with an additional quadratic bubble which ensures local conservation of mass in each tetrahedron. The local space contains the full linear polynomial space and as consequence it provides second order accuracy. In contrast finite volume methods use piecewise constant pressure in each cell and are only first order accurate.

    Pressure @1460 days
    Pressure after 1460 days

    View as VRML97

    (plugin such as Cortona3D is required).

    Pressure Change @1460 days
    Pressure Change after 1460 days

    View as VRML97

    (plugin such as Cortona3D is required).

    Displacement

    The displacements are approximated using standard conforming linear finite elements. They are continous across element boundaries and second order accurate.

    Displacement X @1460 days
    Displacement X after 1460 days
    Displacement Y @1460 days
    Displacement Y after 1460 days
    Displacement Z @1460 days
    Displacement Z after 1460 days

    Strains

    The strains are derived directly from the displacements and are piecewise constant in each element.

    Strain[1,1] @1460 days
    Stain[1,1] after 1460 days
    Strain[1,2] @1460 days
    Stain[1,2] after 1460 days
    Strain[1,3] @1460 days
    Stain[1,3] after 1460 days
    Strain[2,2] @1460 days
    Stain[2,2] after 1460 days
    Strain[2,3] @1460 days
    Stain[2,3] after 1460 days
    Strain[3,3] @1460 days
    Stain[3,3] after 1460 days

    Saturation

    The saturations are resolved using an explicit first order FV method. They are piecewise constant in each cell. A MAPR linear reconstruction may be uploaded at a later stage.

    Saturation Water @1460 days
    Water Saturation after 1460 days

    View as VRML97

    (plugin such as Cortona3D is required).

    Saturation Oil @1460 days
    Oil Saturation after 1460 days

    View as VRML97

    (plugin such as Cortona3D is required).

    Monitor 2

    Default survey - SFR Coarse Cell Pressure Drop Default survey - SFR Well Cell Pressure Drop

    Downloads

    During the this phase all 9 SCA wells and all 6 SRF wells are operated for a period of three years from 01-01-2024 until 31-12-2027.

  • SCA-A: 3000 bpd.
  • SCA-B: 5000 bpd.
  • SCA-C: 10000 bpd.
  • SFR1-E: 7000 bpd decreasing linearly to 3500 bpd.
  • SFR1-W: 6000 bpd decreasing linearly to 3500 bpd.
  • SFR2-E: 4000 bpd decreasing linearly to 2200 bpd.
  • SFR2-W: 6000 bpd decreasing linearly to 3100 bpd.
  • SFR3-E: 1000 bpd decreasing linearly to 600 bpd.
  • SFR3-W: 4000 bpd decreasing linearly to 3000 bpd.

    • The results below are reported at the final time of the simulation (31-12-2027). Wherever available 3D VRML plots are also provided.

    Pressure

    The pressure is computed using modified Arnold-Brezzi finite elements. This a nonconforming Courzeix-Raviart element modified with an additional quadratic bubble which ensures local conservation of mass in each tetrahedron. The local space contains the full linear polynomial space and as consequence it provides second order accuracy. In contrast finite volume methods use piecewise constant pressure in each cell and are only first order accurate.

    Pressure @2555 days
    Pressure after 2555 days
    Pressure Change @2555 days
    Pressure Change after 2555 days
    Pressure Drop @2555 days
    Pressure Drop after 2555 days

    Displacement

    The displacements are approximated using standard conforming linear finite elements. They are continous across element boundaries and second order accurate.

    Displacement X @2555 days
    Displacement X after 2555 days
    Displacement Y @2555 days
    Displacement Y after 2555 days
    Displacement Z @2555 days
    Displacement Z after 2555 days

    Saturation

    The saturations are resolved using an explicit first order FV method. They are piecewise constant in each cell. A MAPR linear reconstruction may be uploaded at a later stage.

    Saturation Oil @2555 days
    Watre Saturation after 2555 days
    Saturation Water @2555 days
    Oil Saturation after 2555 days

    Monitor 3

    Small Leak in to SFR
    Pressure Change after 3650 days with leak
    No Leak
    Pressure Change after 3650 days without leak

    Downloads

    Pressure

    The pressure is computed using modified Arnold-Brezzi finite elements. This a nonconforming Courzeix-Raviart element modified with an additional quadratic bubble which ensures local conservation of mass in each tetrahedron. The local space contains the full linear polynomial space and as consequence it provides second order accuracy. In contrast finite volume methods use piecewise constant pressure in each cell and are only first order accurate.

    Pressure @3650 days Leak
    Pressure after 3650 days
    Pressure Change @3650 days Leak
    Pressure Change after 3650 days
    Pressure Drop @3650 days Leak
    Pressure Drop after 3650 days

    Displacement

    The displacements are approximated using standard conforming linear finite elements. They are continous across element boundaries and second order accurate.

    Displacement X @3650 days
    Displacement X after 3650 days
    Displacement Y @3650 days
    Displacement Y after 3650 days
    Displacement Z @3650 days
    Displacement Z after 3650 days

    Saturation

    The saturations are resolved using an explicit first order FV method. They are piecewise constant in each cell. A MAPR linear reconstruction may be uploaded at a later stage.

    Saturation Water @3650 days Leak
    Water Saturation after 3650 days
    Saturation Oil @3650 days Leak
    Oil Saturation after 3650 days

    Gas Saturation Compare

    SCA B2 Gas Saturation PVT extrapolation.
    PVT Gas saturation
    SCA B2 Gas Saturation PVT restricted extrapolation.
    PVT Gas saturation Restricted

    Downloads

    Pressure

    The pressure after 3650 days is computed using modified Arnold-Brezzi finite elements. This a nonconforming Courzeix-Raviart element modified with an additional quadratic bubble which ensures local conservation of mass in each tetrahedron. The local space contains the full linear polynomial space and as consequence it provides second order accuracy. In contrast finite volume methods use piecewise constant pressure in each cell and are only first order accurate.

    Pressure @3650 days
    Pressure after 3650 days no leak
    Pressure Change @3650 days
    Pressure Change after 3650 days no leak
    Pressure Drop @3650 days
    Pressure Drop after 3650 days no leak

    Displacement

    The displacements are approximated using standard conforming linear finite elements. They are continous across element boundaries and second order accurate.

    Displacement X @3650 days
    Displacement X after 3650 days no leak
    Displacement Y @3650 days
    Displacement Y after 3650 days no leak
    Displacement Z @3650 days
    Displacement Z after 3650 days no leak

    Saturation

    The saturations are resolved using an explicit first order FV method. They are piecewise constant in each cell. A MAPR linear reconstruction may be uploaded at a later stage.

    Saturation Water @3650 days
    Water Saturation after 3650 days no leak
    Saturation Oil @3650 days
    Oil Saturation after 3650 days no leak